Definitions¶
What MAP++ Solves¶
Mooring models can be classified into two groups: static models and dynamic models. Static models ignore the inertia forces and fluid drag loads, and only account for the mean forces in the mooring system, including elasticity, weight (in fluid), and geometric nonlinearities. Static models are the type concerned in MAP++. Extra steps are taken to reformulate the classic single line, closed–form solution [1] into a piece-wise, multi-sgemented system. This piece wise system is composed of a collection of nodes and elements.
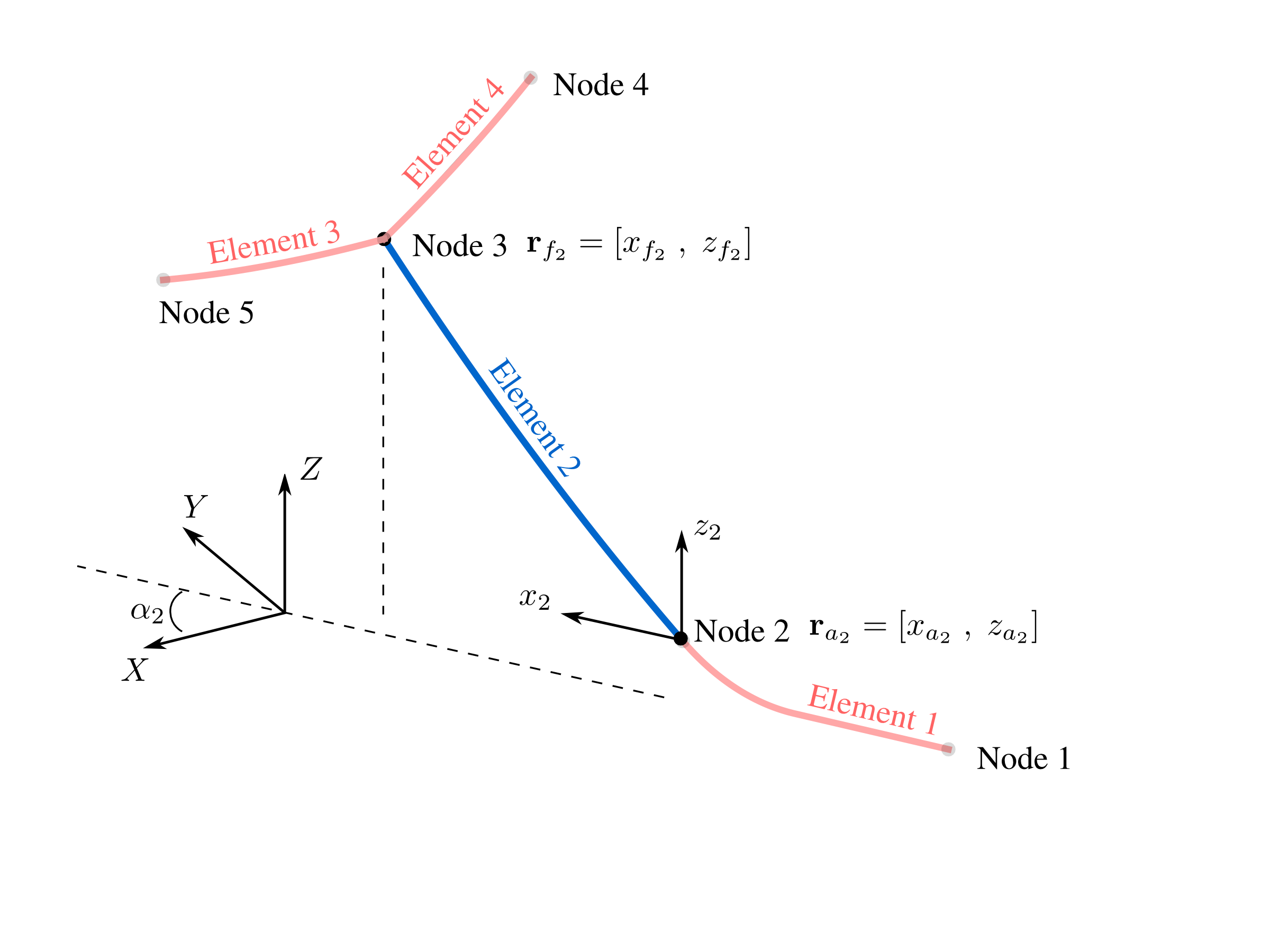
Fig. 1
Each element in Fig. 1 is expressed as a single line counterpart in two configurations. One configuration has the line hanging freely, whereas the second orientation account for friction and contact at the bottom boundary.
Nomenclature¶
| Variable | Definition | Units |
| \(A\) | Cable cross-sectional area | [m^2] |
| \(C_B\) | Seabed contact friction coefficient | – |
| \(E\) | Young’s modulus | [N/m^2] |
| \(g\) | Acceleration due to gravity | [m/s^2] |
| \(h\) | Vertical fairlead excursion | [m] |
| \(H\) | Horizontal fairlead force | [N] |
| \(H_a\) | Horizontal anchor force | [N] |
| \(l\) | Horizontal fairlead excursion | [m] |
| \(L\) | Unstretched line length | [m] |
| \(L_B\) | Line length resting on the seabed | [m] |
| \(M_i\) | Point mass applied to the ith node | [kg] |
| \(r_i\) | Node position vector [xi ; yi ; zi] | [m] |
| \(R_i\) | Rotation angle between the \(x_i\) and \(X\) axis | – |
| \(s\) | Unstretched distance from the anchor (\(0 \leq s \leq L\)) | [m] |
| \(T_j\) | Cable tension vector for the jth elemetn | [N] |
| \(Te(s)\) | Cable tangential tension at distance s | [N] |
| \(V\) | Vertical fairlead force | [N] |
| \(V_a\) | Vertical anchor force | [N] |
| \(w\) | Cable weight-per-unit length in fluid | [N/m] |
| \(x_0\) | Horizontal force transition point for \(H(s)>0\) | [N] |
| \(\rho\) | Fluid density | [kg/m^3] |